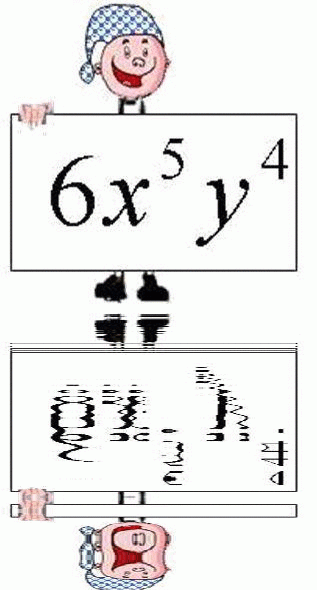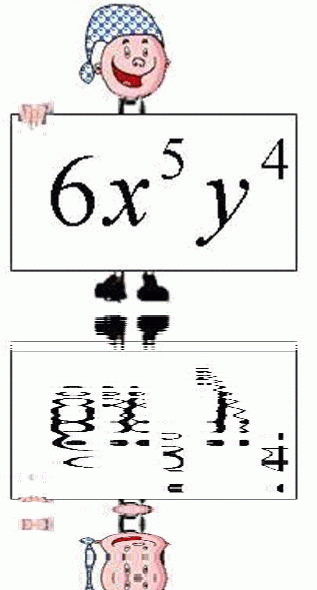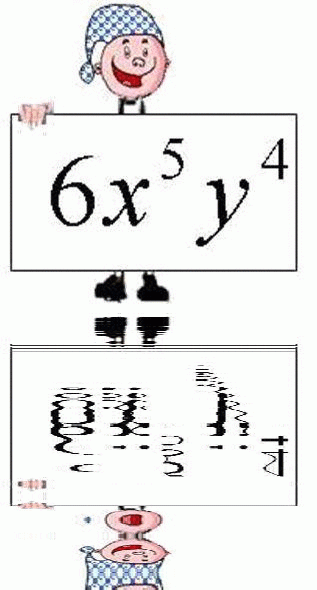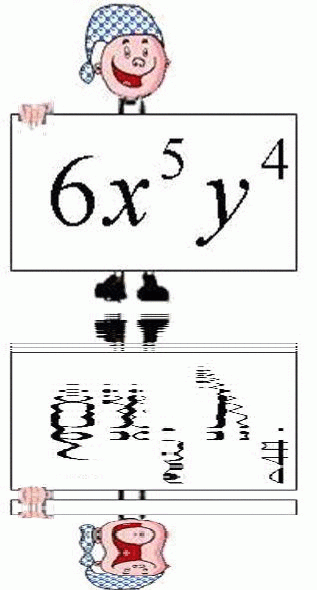
Слышали ли вы об "Одночленах" когда-нибудь? Давайте начнем с ними знакомиться.
Запишите следующие алгебраические выражения.
Если вы ответили правильно, то все выражения, перечисленные здесь, имеют общее имя - одночлены (мономы)
Проанализируйте строение всех этих выражений с2; 2 Пr; П r2 ; 6х5у4; 3х2у . 2х3у3; х5у4; 0,5
х5у4 ; 2ав; 4 . 2ав -и выберите определение одночлена:
1. Выражение, содержащее произведение чисел, переменных и их степеней.
2. Выражение, содержащее произведение переменных.
3. Выражение, содержащее только действия умножения и возведения в
степень.
4. Выражение, содержащее переменную.
5. Выражение, представляющее собой
произведение, множителями которого могут являться числа, одно или несколько
переменных, каждое из которых взято в некоторой степени.
- Как вы считаете, какая из следующих формулировок может быть взята в
качестве одночлена? Какие из них не могут служить определением одночлена?
Прослушайте флеш - ролик и
убедиться в правильности выбранного определения.
Упростите одночлен, 25a3bc(0,2)a2cb2
-Необходимо сгруппировать все числовые
множители, затем все степени с одинаковым основанием и выполнить соответствующие
умножения.
25a3bc(0,2)a2cb2= (25 . 0,2) (а3 а 2) (bb2) (сс)
(25 . 0,2) (а3 а 2)(bb 2) (сс) = 5.а5.b3.с2
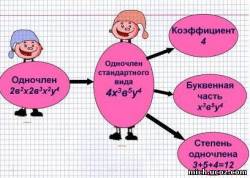
- Итак, 5а5b3с2- стандартный вид
исходного одночлена 25a3bc(0,2)a2cb2
числовой множитель стоит на первом месте и степень любой переменной входит
множителем только один раз, называется одночленом стандартного вида.
-Проще ли стандартный вид одночлена по сравнению с нестандартным?
-Любой ли одночлен можно привести к стандартному виду?
-Преобразуя одночлен, мы фактически получили
алгоритм приведения любого одночлена к стандартному виду!
-В дальнейшем стандартный вид будет служить своеобразной визитной карточкой любого одночлена.
-назовите коэффициент одночлена, буквенную
часть, объясните как найти степень одночлена?
Из предложенных выражений (стандартного,
нулевые, коэффициентом, дробью, степенью, подобными), вставьте пропущенные слова в
следующие определения
1. Одночлен, в котором единственный числовой множитель стоит на
первом месте и степень любой переменной входит множителем только один раз,
называется одночленом …вида.
2. Сумма показателей всех степеней переменных называется
…одночлена.
3. Числовой множитель одночлена стандартного вида называется
…одночлена.
Выполните задания:
№ 1. Из выражений
2ху; 6х2.0,5ху3р; - 5ху; 3x3y3p; 3a2b; a3; 3x5y2(0,2)x2y.
выпишите:
1) одночлены стандартного вида;
2) одночлены нестандартного вида и приведите их к стандартному виду;
№ 2. Запишите примеры:
1) одночленов;
2) выражений, не являющихся одночленами;
3) одночленов стандартного вида;
4) одночленов нестандартного вида.
№ 3. Запишите стандартный
вид следующих одночленов:
1) ххууу=… ; 2) 2.2сссd=…; 3) ах . ах . ах=… ;
4) а . а . а . ... . а=… ;
m раз
№ 4. Найдите числовые
значения одночленов:
1) ab2x=… ; 2) 0,5abxb=… ; 3) 10b2ax=… ; 4) -10axb2… ; 5) - b2ax=….
При a = 2; b = - 3; x = 4. Это задание вы выполните быстро, если
увидите, что…?
Если вы поняли тему, то ответьте на вопросы
1. С какими понятиями вы познакомились при изучении нового материала?
2. Какую формулировку мы с вами взяли в качестве определения одночлена?
3. Приведите примеры одночленов.
4. Являются ли одночленами следующие выражения ? Почему?
5; х; у2в; -2х + 3у; 3ав . 4а2в.
5. .Каждый ли одночлен можно привести к стандартному виду?
Выполни лабораторную работу. Графическое изображение одночленов. Раскраска плоскости
Вы можете перейти на сайт http://interneturok.ru Видеоуроки по основным предметам школьной программы. Смотри и понимай.
Вы можете перейти на сайт Школьный помощник >> http://school-assistant.ru/?predmet=algebra&theme=odnochlen_i_ego_standartni_vid
Школьный помощник — это сервис, который поможет закрепить знания, полученные в школе, или наверстать пропущенный
материал. Выбрав предмет и класс в левом меню, вы попадаете на страницу со списком тем. Перейдя к
соответствующей теме, можно прочесть правила, а также выполнить упражнения или
решить задачи
